Question

simple Brayton cycle using air as the working fluid has a pressure ratio of 10. The minimum and maximum temperatures in the cycle are 295 and 1240 K. Assuming an isentropic efficiency of 83 percent for the compressor and 87 percent for the turbine, determine (a) the air temperature at the turbine exit, (b) the net work output, and (c) the thermal efficiency.

Answer 1

a) 764.45K

b) 210.48 kJ/kg

c) 30.14%

Step-by-step explanation:

pressure ratio = 10

minimum temperature = 295 k

maximum temperature = 1240 k

isentropic efficiency for compressor = 83%

Isentropic efficiency for turbine = 87%

a) Air temperature at turbine exit

we can achieve this by interpolating for enthalpy

h4 = 783.05 kJ/kg ( calculated in the background ) at state 4 using Table A-17 for Ideal gas properties of air

T4 ( temperature at Turbine exit ) = 760 + ( 780 - 760 )
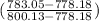`((783.05-778.18)/(800.13-778.18) )` = 764.45K

b) The net work output

first we determine the actual work input to compressor

Wc = h2 - h1 ( calculated values )

= 626.57 - 295.17 = 331.4 kJ/kg

next determine the actual work done by Turbine

Wt = h3 - h4 ( calculated values )

= 1324.93 - 783.05 = 541.88 kJ/kg

finally determine the network output of the cycle

Wnet = Wt - Wc

= 541.88 - 331.4 = 210.48 kJ/kg

c) determine thermal efficiency

лth = Wnet / qin ------ ( 1 )

where ; qin = h3 - h2

equation 1 becomes

лth = Wnet / ( h3 - h2 )

= 210.48 / ( 1324.93 - 626.57 )

= 0.3014 = 30.14%