Question

Consider the integers x and y. When y is divided by x the remainder is 29. When y is divided by x/2, the remainder is 13. Determine x.​

Answer 1

Answer: x = 32

===============================================

Step-by-step explanation:

When we divide y over x to get a remainder of 29, this means we are dividing over a value greater than 29. This means x > 29.

If we divided over a number 29 or less, then the remainder would be smaller than the divisor.

------------------------------------------

The variable x is some integer. When we divide y over (x/2) we get some other integer. This implies that x/2 itself is also an integer. That tells us that x is some even integer.

So far we know that x > 29 and x is some even number.

------------------------------------------

y divided by x leads to a remainder of 29. This means

y/x = q + 29/x

for some integer q, which is the quotient.

Multiply both sides by x

x*(y/x) = x*(q + 29/x)

y = qx + 29

We'll come back to this later.

------------------------------------------

Now divide y over (x/2) to get a remainder 13. We'll let n be the quotient this time

y/(x/2) = n + 13/(x/2)

which is equivalent to

y = n(x/2) + 13

We can multiply both sides by 2 further getting

2y = 2*( n(x/2) + 13 )

2y = nx + 26

Plug in y = qx+29 from earlier

2(qx+29) = nx + 26

2qx + 58 = nx + 26

Let's group the x terms to one side and everything else on the other side

2qx - nx = 26-58

2qx - nx = -32

-nx + 2qx = -32

nx - 2qx = 32

I multiplied both sides by -1 to turn that -32 into 32

Factoring x from the left side gives

nx - 2qx = 32

x(n - 2q) = 32

We have x as an integer, which is stated in the instructions.

In order to have x(n-2q) = 32 be true, this must mean n-2q is an integer.

We can say n-2q = 32/x, so 32/x is some integer because x is an integer.

------------------------------------------

In short, x and n-2q are both integers. In order for the two integers to multiply to 32, the factors must be smaller than 32 or equal to 32.

So
`x \le 32` and
`n-2q \le 32`

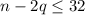
We don't need to worry about the second inequality since all we care about is x.

Recall that earlier we stated that x > 29 and x is even.

Combine this with
`x \le 32` and we form the compound inequality
`29 < x \le 32`

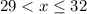
This basically says x is a value from the set {30, 32}

But x = 30 is not a factor of 32. There's no way to have x(n-2q) = 32 be a true equation if x = 30. We must rule x = 30 out.

The only thing left is x = 32. This is the final answer.

------------------------------------------

If x = 32 and y = 29, then we fit the requirements of the problem.

y/x = 29/32 = 0 remainder 29

y/(x/2) = 29/16 = 1 remainder 13

The solution has been confirmed.