Answer:
Peter would be 14. Paul would be 16
Explanation:
Variable labels:
Peter = m, Paul = n
m + n = 24
(m - 5) : (n- 5) = 3:4
The ratio 3:4 in fraction form is

The ration of (m - 5) : (n- 5) in fraction form is
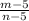
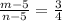
Cross multiply:
4(m - 5) = 3(n - 5)
4m - 20 = 3n - 15
4m = 3n + 5
Find the value of m first:
4m = 3n + 5
m =
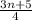
Now going back to the equation m + n = 24, substitute m with
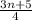 :
:
m + n = 24
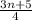 + n = 24
+ n = 24
Solve for n:
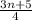 + n = 24
+ n = 24
 + n = 24
+ n = 24
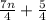 = 24
= 24
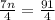
n = 13 (Paul's age)
Solve for m:
m + n = 24
m + 13 = 24
m = 11 (Peter's age)
After three years, Peter would be 11 + 3 = 14 years old and Paul would be 13 + 3 = 16 years old.