Question

Please help me find the value of z.

Answer 1

Answer: z = 12x + 16y - 34

====================================================

Work Shown:

Plug (x,y) = (3,2) into the F(x,y) function

`F(x,y) = 2x^2 + 4y^2\\\\F(3,2) = 2(3)^2 + 4(2)^2\\\\F(3,2) = 34\\\\`

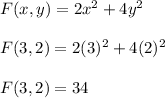
Next, find the gradient and plug in (x,y) = (3,2)

`F(x,y) = 2x^2 + 4y^2\\\\\\\\abla F(x,y) = \Big< (dF)/(dx), (dF)/(dy)\Big>\\\\\\\\abla F(x,y) = \Big< 4x, 8y \Big>\\\\\\\\abla F(3,2) = \Big< 4*3, 8*2 \Big>\\\\\\\\abla F(3,2) = \Big< 12, 16 \Big>\\\\\\`

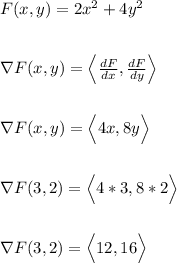
This means,

`z = \\abla F(3,2) \cdot \left(\vec{x} - \big< 3, 2 \big>\right) + F(3,2)\\\\\\z = \\abla F(3,2) \cdot \left(\big< x,y \big> - \big< 3, 2 \big>\right) + F(3,2)\\\\\\z = \\abla F(3,2) \cdot \big< x-3,y-2 \big> + F(3,2)\\\\\\z = \big< 12,16 \big> \cdot \big< x-3,y-2 \big> + 34\\\\\\z = 12(x-3)+16(y-2) + 34\\\\\\z = 12x-36+16y-32 + 34\\\\\\z = 12x+16y-34\\\\\\`

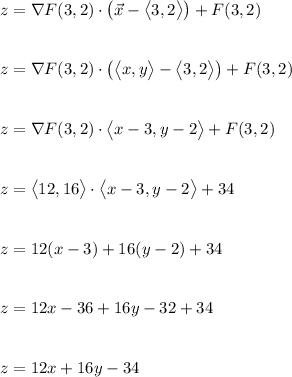
As a way to help check, note how plugging (x,y) = (3,2) into the last equation for z leads to z = 34. This helps confirm that we have the correct equation because the point (3,2,34) must be on F(x,y) and also on z since the plane is tangent to the F(x,y) curve at this point.