Question

car 1 is traveling south at 18 m/s and has a full load, giving it a total mass of 14,650 kg. Car 2 is traveling north at 11 m/s and has a mass of 3,825 kg. After the collision, car 1 has a final velocity of 6 m/s south. What is the velocity of car 2

Answer 1

v_{4}= 80.92[m/s] (Heading south)

Step-by-step explanation:

In order to calculate this problem, we must use the linear moment conservation principle, which tells us that the linear moment is conserved before and after the collision. In this way, we can propose an equation for the solution of the unknown.

ΣPbefore = ΣPafter

where:

P = linear momentum [kg*m/s]

Let's take the southward movement as negative and the northward movement as positive.

`-(m_(1)*v_(1))+(m_(2)*v_(2))=-(m_(1)*v_(3))+(m_(2)*v_(4))`

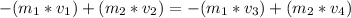
where:

m₁ = mass of car 1 = 14650 [kg]

v₁ = velocity of car 1 = 18 [m/s]

m₂ = mass of car 2 = 3825 [kg]

v₂ = velocity of car 2 = 11 [m/s]

v₃ = velocity of car 1 after the collison = 6 [m/s]

v₄ = velocity of car 2 after the collision [m/s]

`-(14650*18)+(3825*11)=(14650*6)-(3825*v_(4))\\v_(4)=80.92[m/s]`