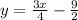Question

Write an equation that represents the line (-2,-6) and (2,-5)

Answer 1

*Correction: The points given on the graph are (-2, -6) and (2, -3)

Answer:

The slope of the line is
`m = (3)/(4) = 0.75`

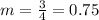
The y-intercept is
`\left(0, - (9)/(2)\right) = \left(0, -4.5\right)`

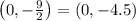
The equation of the line in the slope-intercept form is
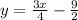`y = (3 x)/(4) - (9)/(2)` 0.75x−4.5

Explanation:

Your input:

Find the equation of a line given two points P=(−2,−6) and
`Q = \left(2, -3\right)Q=(2,-3).`

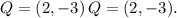
SOLUTION

The slope of a line passing through two points
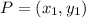`P = \left(x_(1), y_(1)\right)` and
`Q = \left(x_(2), y_(2)\right)`

is given by m =
`(y_(2) - y_(1))/(x_(2) - x_(1))`.

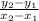We have that ,
`x_(1) = -2`,
`y_(1) = -6y`,
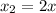`x_(2) = 2x`, and
`y_(2) = -3y`.

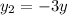Plug the given values into the formula for a slope:
`m = (-3 - \left(-6\right))/(2 - \left(-2\right)) = (3)/(4)`

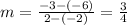
Now, the y-intercept is
`b = y_(1) - m x_(1)` (or
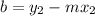`b = y_(2) - m x_(2)` , the result is the same).

`b=-6-((3)/(4))*(-2)=-(9)/(2)`

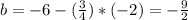
Finally, the equation of the line can be written in the form y = b + m x:

`y = (3 x)/(4) - (9)/(2)`