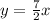Answer:
Equation of line passing through origin and (7,2) is:
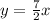
Explanation:
The general form of equation of line is given by:
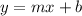
When a line passes through origin it has no y-intercept so the equation will become
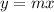
Slope is given by the formula
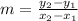
Here,
(x1,y1) = (0,0)
(x2,y2) = (7,2)
Putting the values in the formula
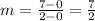
Putting the value of slope in equation of line
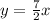
Hence,
Equation of line passing through origin and (7,2) is: