Question

PLLLLEEEEEEAAASSSSSSSSEEEE

help it is easy but I am just tired


Determine which of the lines, if any are perpendicular.


Line a passes through (2, 10) and (4, 13).


Line b passes through (4, 9) and (6, 12).


Line c passes through (2, 10) and (4, 9).

Answer 1

Given:

Line a passes through (2, 10) and (4, 13).

Line b passes through (4, 9) and (6, 12).

Line c passes through (2, 10) and (4, 9).

To find:

Which of the lines, if any are perpendicular.

Solution:

If a line passes through two points, then the slope of line is

`m=(y_2-y_1)/(x_2-x_1)`

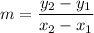
Line a passes through (2, 10) and (4, 13). So, slope of this line is

`m_a=(13-10)/(4-2)=(3)/(2)`

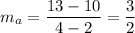
Line b passes through (4, 9) and (6, 12). So, slope of this line is

`m_b=(12-9)/(6-4)=(3)/(2)`

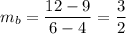
Line c passes through (2, 10) and (4,9). So, slope of this line is

`m_c=(9-10)/(4-2)=(-1)/(2)`

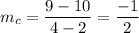
Product of slopes of to perpendicular lines is -1.

`m_a\cdot m_b=(3)/(2)* (3)/(2)=(9)/(4)\\eq -1`

`m_b\cdot m_c=(3)/(2)* (-1)/(2)=(-3)/(4)\\eq -1`

`m_a\cdot m_c=(3)/(2)* (-1)/(2)=(-3)/(4)\\eq -1`

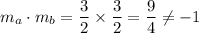
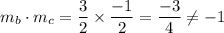
Therefore, any of these lines are not perpendicular to each other.