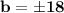Answer:
The values of b are
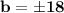
Explanation:
We need to find the value of b will cause
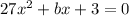 to have one real solution.
to have one real solution.
If it has one real solution, the discriminant is zero.
The formula of discriminant is:
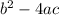
In our case:
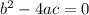
We have a=27, b=b and c=3
Putting values to find b

So, the values of b are