Question

Solve x^2+ 8x- 6=0 using the Quadratic Formula

Answer 1

x=−4+√22 or x=−4−√22

Explanation:

Substitute all values in the quadratic formula.

Solve.

Answer 2

`\boxed {\sf x= {{ - 4\pm √(22) }}}`

Explanation:

The quadratic equation is used to find the roots of a quadratic. The formula is:

`x = \frac{{ - b \pm \sqrt {b^2 - 4ac} }}{{2a}}`

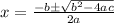
when
`{ax^2 + bx + c = 0}`

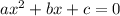
We are given the quadratic:
`x^2+8x-6=0`

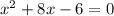
If we compare the given quadratic to the standard form of a quadratic, then:

`a= 1\\b=8 \\c= -6`

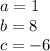
Substitute the values into the formula.

`x = \frac{{ - 8\pm \sqrt {8^2 - 4(1)(-6)} }}{{2(1)}}`

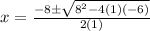
Solve inside the radical first.

Solve the exponent.

• 8²= 8*8= 64

`x = \frac{{ - 8\pm \sqrt {64 - 4(1)(-6)} }}{{2(1)}}`

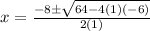
Multiply 4, 1, and -6.

• 4(1)(-6)= 4(-6)= -24

`x = \frac{{ - 8\pm \sqrt {64 - -24}}}{{2(1)}}`

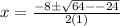
Add 64 and 24 (2 negative signs become a positive)

• 64- -24 64+24=88

`x = \frac{{ - 8\pm \sqrt {88}}}{{2(1)}}`

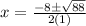
Solve the denominator.

`x = \frac{{ - 8\pm \sqrt {88}}}{{2}}`

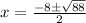
The radical can be simplified. 88 is divisible by a perfect square: 4

`x= \frac{{ - 8\pm \sqrt {4}√(22) }}{{2}}`

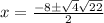
Take the square root of 4.

`x= \frac{{ - 8\pm 2√(22) }}{{2}}`

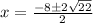
Divide by 2.

`x= {{ - 4\pm √(22) }}`

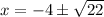
The roots are: x=0.690416 and x=−8.69042