Question

The graph below represents a population

over time. What is the average rate of
change for the function for the interval (6, 12]?
PLS HELP

Answer 1

Average rate of change for the function for the interval (6, 12] is 500 people per year.

Option A is correct.

Explanation:

We need to find the average rate of change for the function for the interval

(6, 12]

The formula used to calculate Average rate of change is:

`Average \ rate \ of \ change=(f(b)-f(a))/(b-a)`

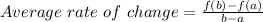
We are given a=6 and b=12

Looking at the graph we can see that when x=6 y= 3000 so, f(a)=3000

and when x=12, y=6000 so, f(b)=6000

Putting values in formula and finding Average rate of change:

`Average \ rate \ of \ change=(f(b)-f(a))/(b-a)\\Average \ rate \ of \ change=(6000-3000)/(12-6)\\Average \ rate \ of \ change=(3000)/(6)\\Average \ rate \ of \ change=500`

So, average rate of change for the function for the interval (6, 12] is 500 people per year.

Option A is correct.