Question

Find the product of all real values of r for which 1/2x=r-x/7

Answer 1

`r = \±\sqrt{14`

`Product = -14`

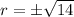
Explanation:

Given

`(1)/(2x) = (r - x)/(7)`

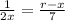
Required

Find all product of real values that satisfy the equation

`(1)/(2x) = (r - x)/(7)`

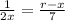
Cross multiply:

`2x(r - x) = 7 * 1`

`2xr - 2x^2 = 7`

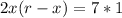
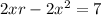
Subtract 7 from both sides

`2xr - 2x^2 -7= 7 -7`

`2xr - 2x^2 -7= 0`

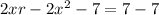
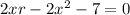
Reorder

`- 2x^2+ 2xr -7= 0`

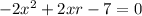
Multiply through by -1

`2x^2 - 2xr +7= 0`

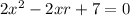
The above represents a quadratic equation and as such could take either of the following conditions.

(1) No real roots:

This possibility does not apply in this case as such, would not be considered.

(2) One real root

This is true if

`b^2 - 4ac = 0`

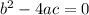
For a quadratic equation

`ax^2 + bx + c = 0`

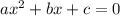
By comparison with
`2x^2 - 2xr +7= 0`

`a = 2`

`b = -2r`

`c =7`

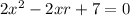
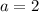
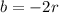
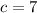
Substitute these values in
`b^2 - 4ac = 0`

`(-2r)^2 - 4 * 2 * 7 = 0`

`4r^2 - 56 = 0`

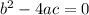
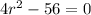
Add 56 to both sides

`4r^2 - 56 + 56= 0 + 56`

`4r^2 = 56`

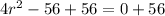
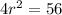
Divide through by 4

`r^2 = 14`

Take square roots

`√(r^2) = \±\sqrt{14`

`r = \±\sqrt{14`

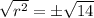
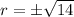
Hence, the possible values of r are:

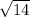`\sqrt{14` or
`-\sqrt{14`

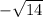
and the product is:

`Product = √(14) * -√(14)`

`Product = -14`