4. What is the solution to the system of equations? Hint: Solve each equation for y first, then graph. 5. What is the solution to the system of equations?

Question

asked Jan 19, 2021 212k views

1 Answer

Adam Singer · Answer 1 · 2021-01-23T15:32:53+0000

Answer:

4. The solution to the system of equations is: (2,-1)

5. The solution to the system of equations is: (3,5)

Explanation:

4. What is the solution to the system of equations?

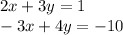
$2x+3y=1\\-3x+4y=-10$

Let:

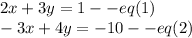
$2x+3y=1--eq(1)\\-3x+4y=-10--eq(2)$

Multiply eq(1) by 3 and eq(2) by 2 and add both equations

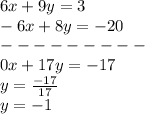
$6x+9y=3\\-6x+8y=-20\\---------\\0x+17y=-17\\y=(-17)/(17)\\y=-1$

So, value of y=-1

Now finding the value of x bu putting value of y in eq(1)

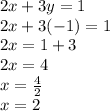
$2x+3y=1\\2x+3(-1)=1\\2x=1+3\\2x=4\\x=(4)/(2)\\x=2$

So, value of x=2

The solution to the system of equations is: (2,-1)

5. What is the solution to the system of equations?

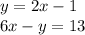
$y=2x-1\\6x-y=13$

Let:

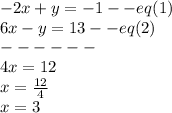
$-2x+y=-1--eq(1)\\6x-y=13--eq(2)\\------\\4x=12\\x=(12)/(4)\\x=3$

So, value of x=3

Putting value of x in equation 1 to find value of y

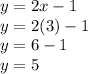
$y=2x-1\\y=2(3)-1\\y=6-1\\y=5$

So, value of y=5

The solution to the system of equations is: (3,5)