Answer:
The nearest option is -3 (negative 3)
So, Option B is correct.
Explanation:
We need to solve the inequality
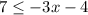
Solving:
Step 1: Switching sides of inequality and reversing the inequality
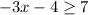
Step 2: Adding 4 on both sides
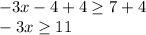
Step 3: Dividing both sides by -3 and reversing the inequality
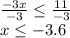
The nearest option is -3 (negative 3)
So, Option B is correct.