Answer:
D) .35
Step-by-step explanation:
m = Mass of block
g = Acceleration due to gravity =
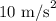
 = Angle of inclination =
= Angle of inclination =
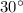
a = Acceleration of block =
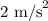
 = Coefficient of friction between the block and the inclined plane
= Coefficient of friction between the block and the inclined plane
f = Frictional force =
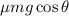
As the forces are conserved in the system we have

The coefficient of friction between the block and the inclined plane is 0.35