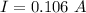Question

A 0.106-A current is charging a capacitor that has square plates 4.60 cm on each side. The plate separation is 4.00 mm.

(a) Find the time rate of change of electric flux between the plates in V·m/s
(b) Find the displacement current between the plates in A

Answer 1

a

`(d \phi_(E))/(dt) =1.1977 *10^(10) \ V\cdot m/s`

b

`I = 0.106 \ A`

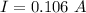
Step-by-step explanation:

From the question we are told that

The current is
`I = 0.106 \ A`

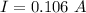
The length of one side of the square
`a = 4.60 \ cm = 0.046 \ m`

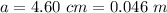
The separation between the plate is
`d = 4.0 mm = 0.004 \ m`

Generally electric flux is mathematically represented as

`\phi_E = (Q)/(\epsilon_o)`

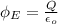
differentiating both sides with respect to t is

`(d \phi_(E))/(dt) = (1)/(\epsilon_o) * (d Q)/( dt)`

=>
`(d \phi_(E))/(dt) = (1)/(\epsilon_o) *I`

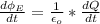
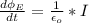
Here
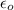`\epsilon_o` is the permitivity of free space with value

`\epsilon _o = 8.85*10^(-12) C/(V \cdot m)`

=>
`(d \phi_(E))/(dt) = (0.106)/(8.85*10^(-12))`

=>
`(d \phi_(E))/(dt) =1.1977 *10^(10) \ V\cdot m/s`

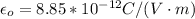
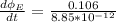
Generally the displacement current between the plates in A

`I = 8.85*10^(-12) * 1.1977 *10^(10)`

=>
`I = 0.106 \ A`