
★ Sofian's current age is (2x + 3) times Mastura's age.
★ Mastura's current age is (x + 5) years
★ 6 years ago, the sum of their ages is 44 years.

★ The value of x.

According to the question,
Present age of Mastura = (x + 5) years
Present age of Sofian = (2x + 3) (x + 5) years, i.e :
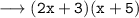
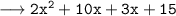

Now,
Mastura's age 6 years ago = (x + 5) - 6
=> x + 5 - 6
=> x - 1
Sofian's age 6 years ago = 2x² + 13x + 15 - 6
= 2x² + 13x + 9
Using the condition provided by the question,
Mastura's age 6 years ago + Sofian's age 6 years ago = 44

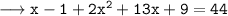
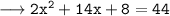

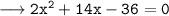
• Taking "2" common.
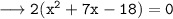
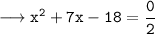

• Using splitting the middle term

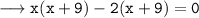
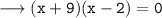
either
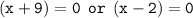

[As the age cannot be negative. So x = - 9 is rejected]
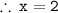

According to the condition provided by the question,
• Mastura's age 6 years ago + Sofian's age 6 years ago = 44
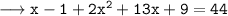
Putting x = 2 we get,
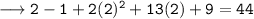
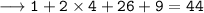
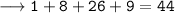
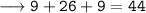
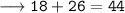
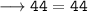
Hence verified.

Hope it helps you! :))