Answer:
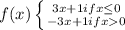
Explanation:
So if we first graph the given equation, we'll see the graph I've attached below.
Remember that piecewise functions are functions that change based on the circumstances. I know that sounds super confusing, but it's actually really simple!
In this case, for example, we see the line increasing from -∞ to
, and then suddenly going downwards and decreasing. That's a good spot for us to notice because that indicates a change. We notice that the function looks different when
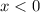or
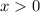. If you break the function into those two parts, you see that they are just linear equations, but they're only visible when x is either greater than or less than 0.
Now that we notice this pattern, we can find the equation of the lines for both lines.
The points (-3,-8) and (-1,-2) are points on the first line, the one that increases (on the left). We can use those points to find the slope of the first line. Remember the slope equation:
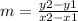
Plug in your points:
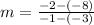
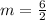
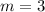
So, the slope of the first line is 3. The y-intercept, looking at the graph, is 1. The equation of the first line is
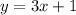. We'll need this later.
Let's do the same thing for the second line. Just looking at the graph, we can see that this is the same exact line, just with a negative slope. So, the equation for the second line is
.
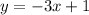So now we can set up a piecewise function.
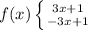
The two functions in the bracket are the two different functions used in this graph. Now we need to figure out where each function is effective. Well, they share a y-intercept. Remember that a true function cannot have two points with the same x value. So the first function is effective to the left of x=0, while the second is effective to the right of x=0. In other words, when
,
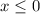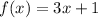. But, when
,
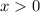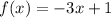. Now our piecewise function looks like this:
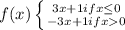
And that is our piecewise function for the original function.
I know this is confusing, so please let me know if you have any questions! I hope this helps!