Question

Find the perimeter of quadrilateral ABCD with vertices A(-2,-2), B(-1,3),

C(5, 3), and D(4, -2).

Answer 1

22.2

Explanation:

Step one

given the coordinates

ABCD with vertices A(-2,-2), B(-1,3), C(5, 3), and D(4, -2)

AB=(-2,-2),(-1,3)

BC=(-1,3), (5, 3)

CD=(5, 3),(4, -2)

DA=(4, -2),(-2,-2)

The distance between points AB=

`AB= \sqrt (x_2-x_1)^2+(y_2-y_1)^2`

`AB= \sqrt (-1+2)^2+(3+2)^2\\\\AB= \sqrt 1^2+(5)^2\\\\AB= \sqrt26\\\\AB=5.1`

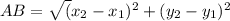
The distance between points BC=

`BC= \sqrt (5+1)^2+(3-3)^2\\\\BC= \sqrt 6^2+(0)^2\\\\BC= \sqrt36\\\\BC=6`

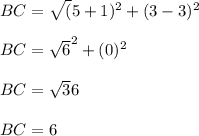
The distance between points CD

`CD= \sqrt (4-5)^2+(-2-3)^2\\\\CD= \sqrt -1^2+(-5)^2\\\\CD= \sqrt26\\\\CD=5.1`

The distance between points DA

`DA= \sqrt (4+2)^2+(-2+2)^2\\\\DA= \sqrt 6^2+(0)^2\\\\DA= \sqrt36\\\\DA=6`

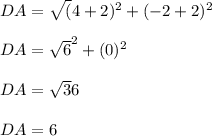
Hence the perimeter = 5.1+6+5.1+6

= 22.2