Answer:
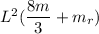
Step-by-step explanation:
m = Mass of each rod
L = Length of rod = Radius of ring
 = Mass of ring
= Mass of ring
Moment of inertia of a spoke
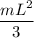
For 8 spokes
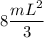
Moment of inertia of ring
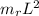
Total moment of inertia
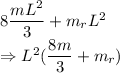
The moment of inertia of the wheel through an axis through the center and perpendicular to the plane of the ring is
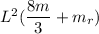 .
.