Question

Use the function f (x) = 2x^2 – 5.

(Look at picture)

Answer 1

C

Explanation:

By the definition of an inverse function, if:

`f(a)=b\text{ then } f^(-1)(b)=a`

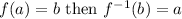
Therefore, the domain of the original function will be the range of the inverse function.

And the range of the original function will be the domain of the inverse function.

We have the original function:

`f(x)=2x^2-5`

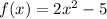
With the domain:

`-\infty<x<\infty`

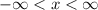
Since the domain of the original function is such, then the range of the inverse function is also the same as above.

So, the range of the inverse function is also:

`-\infty< f^(-1)(x)< \infty`

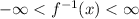
So, our answer is

C.

Notes:

A, B, and E would automatically be incorrect since we never use ”or equal to” when using the infinity symbol. This is because we can never “equal” infinity.