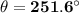Answer:
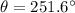
Explanation:
Complex Numbers
They are expressed as the sum of a real part and an imaginary part:
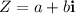
Complex numbers can also be expressed in polar form:
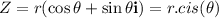
Where r is the modulus of the complex number and θ is the argument.
The argument can be calculated by:
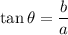
The angle θ must be calculated in the appropriate quadrant depending on the signs of the real and imaginary parts.
The complex number is given as:
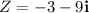
Here: a=-3, b=-9
Since both components are negative, the argument lies in the third quadrant (180° < θ < 270°).
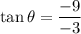
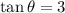
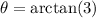
The calculator gives the answer 71.6°, we need to adjust the angle to the third quadrant by adding 180°, thus