Answer:
![4\le \:y+2\le \:-3\left(y-2\right)+24\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:2\le \:y\le \:7\:\\ \:\mathrm{Interval\:Notation:}&\:\left[2,\:7\right]\end{bmatrix}](https://img.qammunity.org/2021/formulas/mathematics/high-school/dr83t23pwqh3ea1ccdvfn3oi1yjb88da30.png)
The solution graph is also attached.
Explanation:
Given
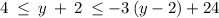
as
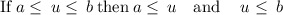
so
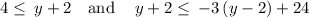
solving the intervals
as
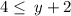
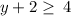
subtract 2 from both sides
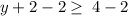
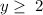
also
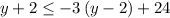
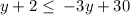
subtract 2 from both sides
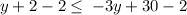
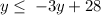
Add 3y to both sides
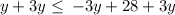
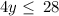
Divide both sides by 4
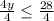
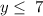
so combining the intervals
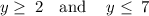
Merge overlapping intervals
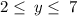
Therefore,
![4\le \:y+2\le \:-3\left(y-2\right)+24\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:2\le \:y\le \:7\:\\ \:\mathrm{Interval\:Notation:}&\:\left[2,\:7\right]\end{bmatrix}](https://img.qammunity.org/2021/formulas/mathematics/high-school/dr83t23pwqh3ea1ccdvfn3oi1yjb88da30.png)
The solution graph is also attached.