Question

The population of algae in an experiment increases by 30% each day. If there were 100 algae at the beginning, predict the number of algae after 5 days.

Future Amount = [?] algae
Round to the nearest whole number.

Answer 1

About 371

Explanation:

This question is showing exponential growth, so use the formula a(b)^x, where a is the initial value, and b is the rate(as a decimal is working with percents). X is the time.

a=100

b=30% increase each day means 1.3 as a decimal

plug that in

100(1.3)^x

That's our exponential formula:
`100(1.3)^x`

To find the number of algae after 5 days, plug in x for 5.

`100(1.3)^5`

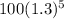
Evaluate (never round until the very end): 100(3.71293)

Further evaluate(now round to nearest whole number): ≈ 371

Therefore, the population is about 371 algae.