Answer:
0.667 m/s
Step-by-step explanation:
Given that,
Mass of a rubber bullet, m₁ = 20 g = 0.02 kg
Initial speed of rubber bullet, u₁ = 60 m/s
Mass of the wood block, m₂ = 3 kg
Initial speed of the wooden block, u₂ = 0
A rubber bullet hits the stationary wood block. The rubber bullet ricochets off the wood block with a velocity of 40.0 m/s in the opposite direction.
Final speed of rubber bullet, v₁ = -40 m/s
Using the conservation of momentum. It will remains conserved. Let v₂ is the velocity of the wood block.
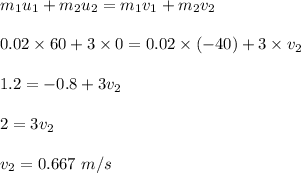
So, the velocity of the wood block is 0.667 m/s.