Answer: 90,75. cos 55°. sin55° ≈ 42,64
through E, draw EK perpendicular to BC (F ∈ BC)
because E is the midpoint of AB => BE = 11/2 = 5.5
ΔBEF is a right triangle at K
=> sin 55° = EK/BE
=> EK = 5,5.sin 55°
ΔABC has E and F is the midpoints of AB and AC
=> EF is the median line of the triangle
=> EF = 1/2.BC
through A, draw AD perpendicular to BC
=> ΔABD is a right triangle at D
=> BC = 11.cos 55°.2 = 22.cos 55°
=> EF = 11.cos 55°
=>the area of the trapezium BEFC is:
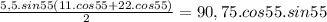
Explanation: