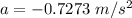Question

Find deacceleration An engineer in a locomotive sees a car stuck on the track at a railroad crossing in front of the train. When the engineer first sees the car, the locomotive is 360 m from the crossing and its speed is 16 m/s. If the engineer’s reaction time is 0.53 s, what should be the magnitude of the minimum deceleration to avoid an accident? Answer in units of m/s^2

Answer 1

The deceleration is
`a = -0.7273 \ m/s^2`

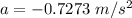
Step-by-step explanation:

From the question we are told that

The distance of the car from the crossing is
`d = 360 \ m`

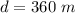
The speed is
`u = 16 \ m/s`

The reaction time of the engineer is
`t = 0.53 \ s`

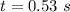
Generally the distance covered during the reaction time is

`d_r = u * t`

=>
`d_r = 16 * 0.53`

=>
`d_r = 8.48 \ m`

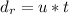
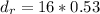
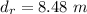
Generally distance of the car from the crossing after the engineer reacts is

`D = d- d_r`

=>
`D = 360 - 8.48`

=>
`D = 352 \ m`

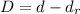
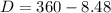
Generally from kinematic equation

`v^2 = u^2 + 2as`

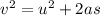
Here v is the final velocity of the car which is 0 m/s

So

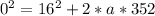
`0^2 = 16^2 + 2 * a * 352`

=>
`a = -0.7273 \ m/s^2`