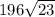Answer:
(i) √23
(ii) 196√23
General Formulas and Concepts:
Pre-Algebra
- Order of Operations: BPEMDAS
Algebra I
- Standard Form: ax² + bx + c = 0
- Quadratic Formula:
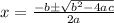
Explanation:
Step 1: Define
Standard Form: x² - 10x + 2 = 0
Step 2: Define variables
a = 1
b = -10
c = 2
Step 3: Find roots
- Substitute:
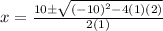
- Exponents:
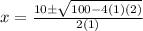
- Multiply:
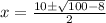
- Subtract:
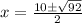
- Simplify:
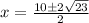
- Factor:
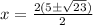
- Divide:
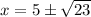
Step 4: Define roots
α > β
α = 5 + √23
β = 5 - √23
Step 5: Evaluate
i
- Substitute:
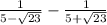
- Subtract:
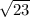
ii
- Substitute:

- Evaluate:

- Subtract: