Answer:
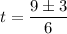


Explanation:
s = Speed of Emile = 6 miles/hour
d = Distance traveled by Emile =
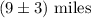
Time taken to find the minimum and maximum time Emile ran for is
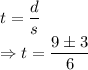
The required equation is
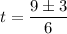
The time taken is
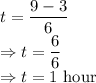
The minimum number of hours Emile runs is 1 hour.
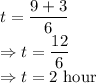
The maximum number of hours Emile runs is
 .
.