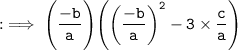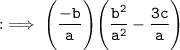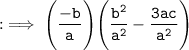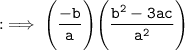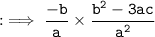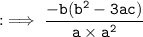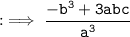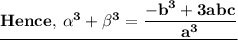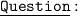
If α and β are the roots of the equation ax² + bx + c = 0, where a, b and c are constants such that a ≠ 0, find in terms of a, b and c expressions for :
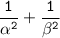
- α³ + β³


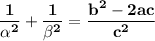
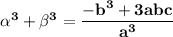

As, α and β are the roots of the equation ax² + bx + c = 0
We know that :
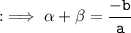
and
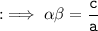

Now, let's solve given values :
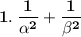
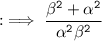
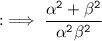

Now, by using identity :
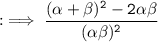

Now, by substituting values of :
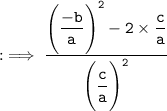
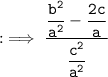
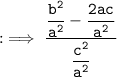
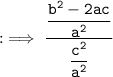
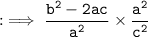
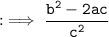

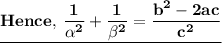

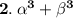

By using identity :
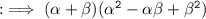
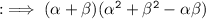

By using identity :
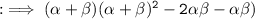
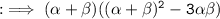

Now, by substituting values of :