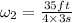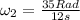Answer:
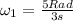 and
and
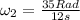
Explanation:
Given that the larger gear is turning at the rate 50rpm. The angular velocity,
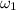 , of the larger gear can be calculated as follows:
, of the larger gear can be calculated as follows:
 to convert that to secs, we know that 1 rev = 2πRad and 60secs make a min, so we have:
to convert that to secs, we know that 1 rev = 2πRad and 60secs make a min, so we have:
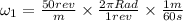
That gives
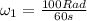
Which gives:
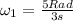
This is the angular velocity of the larger gear in rads/sec.
In order to get the angular velocity of the smaller gear, we know from the question that both gear are connected to the same belt. This implies that they have the same linear velocity. Thus let us find the linear velocity of the larger gear. This is given by
 where v stands for linear velocity and
where v stands for linear velocity and
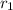 for radius of larger velocity.
for radius of larger velocity.
We are given the radius of the larger gear as 7ft so we have

To get the angular velocity of the smaller gear, we use
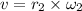 where
where
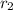 is the radius of the smaller gear which is given as 4.
is the radius of the smaller gear which is given as 4.
Since linear velocity is the same, we have