Question

Suppose a box contains 10 coins, where three of them are type-A and seven of them are type-B. The probability of head is 0.4 if we toss a type-A coin and 0.6 for a type-B coin. One person chooses one coin at random and tosses it three times. What is the probability that this coin is type-A if the outcome is two heads out of three tosses?

Answer 1

0.222

Explanation:

Given that:

For Type A coins = 3

The probability of head in a type A coin i.e. (p) = 0.4

Then, the probability of getting a tail (q) = 1 - p = 1 - 0.4 = 0.6

For Type B coins = 7

The probability of head in a type B coin i.e. (p) = 0.6

Then, the probability of getting a tail (q) = 1 - p = 1 - 0.6 = 0.4

One person who tosses a coin three times get a probability of obtaining a head twice.

Using, the formula:

=
`^nC_r * p^r * q^(n-r)`

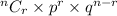
For Type A coin;

The probability of getting two heads in three tosses is:

`= ^3C_2 * 0.4^2 * 0.6^(1)`

`=(3!)/(2!(3-2)!) * 0.4^2 * 0.6^1`

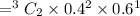
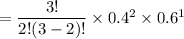
= 0.288

For Type B coin;

The probability of getting two heads in three tosses is:

`= ^3C_2 * 0.6^2 * 0.4^(1)`

`=(3!)/(2!(3-2)!) * 0.6^2 * 0.4^1`

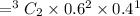
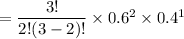
= 0.432

Since we have two heads out of three tosses, the probability that the coin is type A is = (P) of choosing coin A × (P) of obtaining two heads from three tosses) / total probability of getting two heads from three tosses.

However;

(P) of choosing coin A = 3/10 = 0.3

(P) of choosing coin B = 7/10 = 0.7

∴

Given that, we obtain two head from three tosses, the (P) that the coin type is A is:

`= ((0.3 * 0.288))/( (0.3 * 0.288 + 0.7 * 0.432))`

`= ((0.0864))/( (0.0864 + 0.3024))`

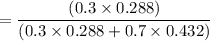
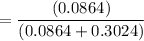
= 0.222