Question

A doctor examines a mole with a 15.0 cm focal length magnifying glass held 12.4 cm from the mole.

a. What is its magnification?
b. Where is the image?
c. How big is the image of a 5.00 mm diameter mole?

Answer 1

a. Magnification = 6.1

b. The image formed is virtual, and on the same side of the lens as the object.

c. Image size = 119.8 squared millimetres

Step-by-step explanation:

Magnification =
`(Image distance)/(Object distance)`

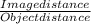
But, focal length, f = 15.0 cm, and object distance, u = 12.4 cm. Let the image distance be represented by v.

a. Applying the lens formula, we have;

`(1)/(f)` =
`(1)/(u)` +
`(1)/(v)`

`(1)/(15)` =
`(1)/(12.4)` +
`(1)/(v)`

`(1)/(v)` =
`(1)/(15)` -
`(1)/(12.4)`

= -
`(13)/(930)`

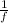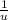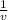
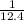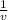
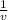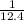
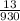
v = -75.1538

The image distance, v = -75.2 cm

Magnification =
`(75.2)/(12.4)`

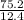
= 6.0645

Magnification = 6.1

b. The image formed is virtual, and on the same side of the lens as the object.

c. Given that diameter of mole = 5.00 mm.

Its radius =
`(diameter)/(2)` =
`(5.0)/(2)`

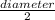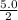
= 2.5 mm

Thus, the area of the mole would be;

A =
`\pi`
`r^(2)`

=
`(22)/(7)` x
`(2.5)^(2)`

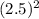
= 19.643

A = 19.64 square millimetres.

Thus, the size of the image can be determined by;

Magnification =
`(Image size)/(Object size)`

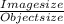
Image size = Magnification x object size

= 6.1 x 19.64

= 119.804

The size of the image is 119.8 squared millimetres.