Question

Find the volume of a smaller wedge cut from a sphere of radius 66 by two planes that intersect along a diameter at an angle of π/6

Answer 1

The answer is "
`(\pi a^3)/(9)`".

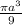Explanation:

please find the complete question in the attached file.

Let the sphere center be (0,0,0) and then let the intersection diameter lie all along the z-axis.

So one of the collision plans is the xz-plane the other is the path via an xz-plane angle.

`\theta = (\pi)/(6)`

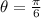
All appropriate region could then be indicated in spherical coordinates

`E= {(\rho, \theta, \phi) : 0 \geq \rho \geq a, 0 \geq \theta \geq (\pi)/(6), 0 \geq \phi \geq \pi }`

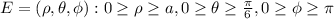
Calculating the volume:

`\to v(E)=\int \int_(E) \int dV\\`

`=\int_(0)^{(\pi)/(6)} \int_(0)^(\pi) \int_(0)^(a) \rho^2 \sin \phi d \rho d \phi d \theta\\\\ =\int_(0)^{(\pi)/(6)} d \theta \int_(0)^(\pi) \sin \phi d \int_(0)^(a) \rho^2 d \rho\\\\= [\theta]^{(\pi)/(6)}_(0) [-\cos \phi]^(\pi)_(0) [(\rho^3)/(3)]^(a)_(0)\\\\= (\pi)/(6) [1+1] (a^3)/(3)\\\\=(\pi a^3)/(9)`