Question

A rectangular channel 3-m-wide carries 12 m^3/s at a depth of 90cm. Is the flow subcritical or supercritical? For the same flowrate, what depth will five critical flow?

Answer 1

Super critical

1.2 m

Step-by-step explanation:

Q = Flow rate =
`12\ \text{m}^3/\text{s}`

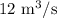
w = Width = 3 m

d = Depth = 90 cm = 0.9 m

A = Area = wd

v = Velocity

g = Acceleration due to gravity =
`9.81\ \text{m/s}^2`

`Q=Av\\\Rightarrow v=(Q)/(wd)\\\Rightarrow v=(12)/(3* 0.9)\\\Rightarrow v=4.44\ \text{m/s}`

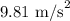
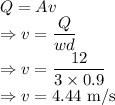
Froude number is given by

`Fr=(v)/(√(gd))\\\Rightarrow Fr=(4.44)/(√(9.81* 0.9))\\\Rightarrow F_r=1.5`

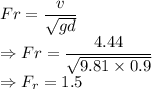
Since
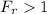`F_r>1` the flow is super critical.

Flow is critical when
`Fr=1`

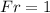
Depth is given by

`d=((Q^2)/(gw^2))^{(1)/(3)}\\\Rightarrow d=((12^2)/(9.81* 3^2))^{(1)/(3)}\\\Rightarrow d=1.2\ \text{m}`

The depth of the channel will be 1.2 m for critical flow.