Question

An engineer who is now 65 years old began planning for retirement 40 years ago. At that time, he thought that if he had $1 million when he retired, he would have more than enough money to live his remaining life in luxury. Assume the inflation rate over the 40-year time period averaged a constant 4% per year.

Required:
a. What is the CV purchasing power of his $1 million at age 65?
b. How many future dollars should he have accumulated over the 40 years to have a CV purchasing power equal to $1.9 million at his current age of 65?

Answer 1

The answer is "$208,289.045 and $9,121,939.2"

Step-by-step explanation:

In point a:

40 years before CV buying power:

`= \frac{\$ \ 1,000,000}{(1 + 4.00\%) ^ {40}}\\\\= (\$ \ 1,000,000)/(4.80102063)\\\\= \$ \ 208,289.045`

CV buying power was $208,289.045 and for 40 years before the start of each year forty years ago.

In point b:

Power CV = $1.9 million

Future accumulated value:

`= \$ \ 1,900,000 * (1 + 4.00 \%) ^ {40}\\\\= \$ \ 1,900,000 * 4.80102063\\\\= \$ \ 9,121,939.2`

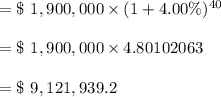
The future accumulated value will be= $9,121,939.2.