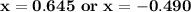Answer:
After solving
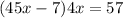 we get
we get
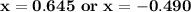
Explanation:
We need to solve the equation:
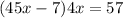
Solving:
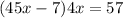
Multiply 4x with terms inside the bracket
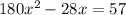
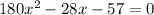
We need to solve above equation to find value of x
Using quadratic formula for finding value of x:
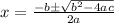
We have a=180, b=-28 and c=-57

Values of x are
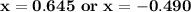
So, After solving
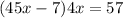 we get
we get