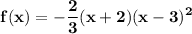Question

Write a function using the graph ​

Answer 1

`\displaystyle f(x)=-(2)/(3)(x+2)(x-3)^2`

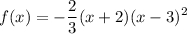
Explanation:

The graph corresponds to a cubic function of the form:

`f(x)=a(x-p)(x-q)(x-r)`

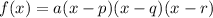
Where p, q, and r are the zeros of f(x).

We can clearly see there are only two crossings through the x-axis. That is because one of the roots is repeated (multiple).

Thus, the roots are p=-2, q=r=3

Substituting into the function:

`f(x)=a(x+2)(x-3)(x-3)`

`f(x)=a(x+2)(x-3)^2`

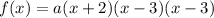
The value of a can be found by using the y-intercept seen on the graph (0,-12):

`-12=a(0+2)(0+3)^2`

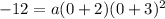
Operating:

`-12=18a`

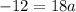
Thus:

`a = -12 / 18 = -2/3`

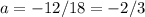
The function is now complete:

`\mathbf{\displaystyle f(x)=-(2)/(3)(x+2)(x-3)^2}`