Question

What is the predicted change in the boiling point of water when 1.50 g of

barium chloride (BaCl₂) is dissolved in 1.50 kg of water?
Kb of water = 0.51°C/mol
molar mass BaCl₂ = 208.23 g/mol
ivalue of BaCl₂ = 3

Answer 1

0.00735°C

Step-by-step explanation:

By seeing the question, we can see the elevation in boiling point with addition of BaCl₂ in water

⠀

`\textsf {While} \: \sf {\Delta T_b} \: \textsf{expression is used} \\ \textsf {for elevation of boiling point}`

⠀

⠀

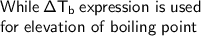
The elevation in boiling point is a phenomenon in which there is increase in boiling point in solution, when the particular type of solute is added to pure solvent.

⠀

⠀

`\sf \large \underline{The \: formula \: to \: be \: used \: in \: this \: question \: is} \\ \boxed{T_b = i * K_b * m}`

⠀

⠀

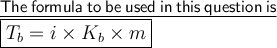
Where 'i' is van't hoff factor which represents the ratio of observed osmotic pressure and the value to be expected.

and 'i' is 3 (as given in the question)

⠀

'Kb' is molal boiling point constant. And it's value is 0.51°C/mol(given in question)

⠀

'm' represent the molality of solution. Molatity is no. of moles of solution present in 1kg of solution.

⠀

⠀

To find molality, we have to divide no. of moles of solute by weight of solution

⠀

While first we need to no. of moles

`\sf \implies no. \: of \: moles = (weight \: of \: solute)/(molar \: mass \: of \: solute) \\ \\ \implies \sf no. \: of \: moles = (1.5)/(208.23) \\ \\ \sf \implies no. \: of \: moles = 0.0072`

⠀

⠀

Now, we will find molality

⠀

`\sf \hookrightarrow molality = (no.\: of \: moles)/(weight \: of \: solution) \\ \\ \sf \hookrightarrow molality = (0.072)/(1.5) \\ \\ \sf \hookrightarrow molality = 0.048 \: mol {kg}^( - 1)`

⠀

⠀

`\textsf{ \large{ \underline{Now substituting the required values}}}`

⠀

`\sf \longmapsto \Delta T_b = 3 * 0.51 * 0.0048 \\ \\ \\ \boxed{ \tt{ \longmapsto \Delta T_b =0.00735{ \degree}C}}`

⠀

⠀

⠀

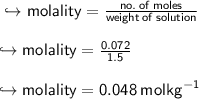
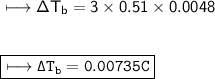
Henceforth, the change in boiling point is 0.00735°C.