Answer:
The ball will reach a maximum height of 39.993 meters after 1.428 seconds.
Explanation:
Let suppose that no non-conservative forces acts on the ball during its motion, then we can determine the maximum height reached by the Principle of Energy Conservation, which states that:
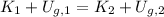 (1)
(1)
Where:
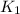 ,
,
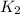 - Initial and final translational kinetic energies, measured in joules.
- Initial and final translational kinetic energies, measured in joules.
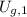 ,
,
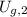 - Initial and final gravitational potential energies, measured in joules.
- Initial and final gravitational potential energies, measured in joules.
By definition of translational kinetic energy and gravitational potential energy we expand and simplify the expression above:
 (2)
(2)
Where:
 - Mass of the ball, measured in kilograms.
- Mass of the ball, measured in kilograms.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
 ,
,
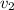 - Initial and final speed of the ball, measured in meters per second.
- Initial and final speed of the ball, measured in meters per second.
 ,
,
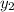 - Initial and final heights of the ball, measured in meters.
- Initial and final heights of the ball, measured in meters.
The final height of the ball is determined by the following formula:

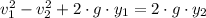
 (3)
(3)
If we know that
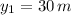 ,
,
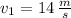 ,
,
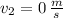 and
and
 , the maximum height that the ball will reach is:
, the maximum height that the ball will reach is:
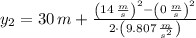
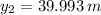
The ball will reach a maximum height of 39.993 meters.
Given the absence of non-conservative forces, the ball exhibits a free fall. The time needed for the ball to reach its maximum height is computed from the following kinematic formula:
 (4)
(4)
If we know that
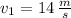 ,
,
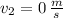 and
and
 , then:
, then:
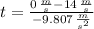
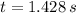
The ball will take 1.428 seconds to reach its maximum height.