Question

Suppose that the number of patients on the kidney waiting list from 2003 to 2010 can be modeled by the equation ​, where x0 represents the year 2000. Assume that this trend continues and predict the year in which patients will be on the waiting list.

The year in which patients will be on the waiting list is
nothing.
​(Simplify your answer. Round to the nearest year as​ needed.)

Answer 1

The question is missing parts. Here is the complete question.

Suppose that the number of patients on the kidney waiting list from 2003 to 2010 can be modeled by the equation
`y=201x^(2)-2813x+52267`, where x₀ represents the year 2000. Assume that this trend continues and predict the year in which 71,381 patients will be on the waiting list.

Answer: The year in which 71,381 patients will be on the waiting list is 2019.

Explanation: y represents the amount of patients waiting on the list. x is in years.

To determine how many years for that amount of patients, we substitute y by 71,381:

`y=201x^(2)-2813x+52267`

`71381=201x^(2)-2813x+52267`

`201x^(2)-2813-19114=0`

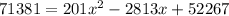
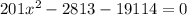
Solving the quadratic equation:

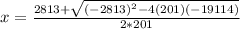
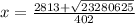
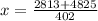`x=\frac{2813+\sqrt{(-2813)^(2)-4(201)(-19114)} }{2*201}`

`x=(2813+√(23280625) )/(402)`

`x=(2813+4825)/(402)` = 19

`x=(2813-4825)/(402)= -5.005`

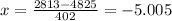
The quadratic equation will give two solutions, but one of them is negative. Since there is no amount of negative time, the result is 19.

The initial year (x₀) is 2000. It will need 19 years for the patients to be 71,381, which means that the year is 2019.