Question

the weights of steers in a herd are distributed normally. the standard deviation is 200lbs and the mean steer weight is 1400lbs. find the probability that the weight of a randomly selected steer is less than 1859lbs

Answer 1

The probability that the weight of a randomly selected steer is less than 1859lbs is 0.9890

Explanation:

Given

Mean = 1400 lbs

SD = 200 lbs

In order to find the probability of a random variable x we have to find the z-score of the data point.

z-score is calculated by:

`z = (x-mean)/(SD)`

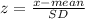
Putting x=1859

`z = (1859-1400)/(200)\\z = (459)/(200)\\z = 2.295`

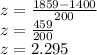
The z-score for 1859 is 2.295

We have to use the z-score table to find the required probability

So,

`P(z<2.295)\ or\ P(x<1859) = 0.9890`

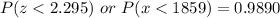
Hence,

The probability that the weight of a randomly selected steer is less than 1859lbs is 0.9890