Answer:
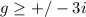
Explanation:
Using clues given in the problem, we can set up a solvable inequality.
A number g squared:
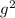
The sum of a number g squared and 4:
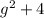
Is greater than or equal to:
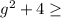
Greater than or equal to -5:
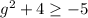
Isolate
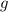 :
:
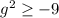
Solve for
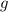 :
:
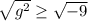
This^ looks bad because of the negative, but as I'll show you in the next step it can be split up and you will use the value
 , or
, or
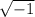 .
.
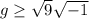
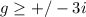
I hope this helps!