Answer:
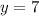
Explanation:
First, let's use the two given points to find the slope. Remember the slope equation:
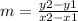
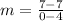
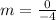
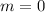
If we're following slope-intercept form, what we have so far is

Substitute one of the given points for the
 and
and
 values in order to find
values in order to find
 :
:
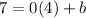
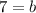
Now, if we put that back into our slope-intercept equation we get
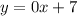
or,
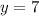
Right off the bat, we can see how we ended up with this equation because both points have the same y-values. This indicates a horizontal line.
I hope this helps!