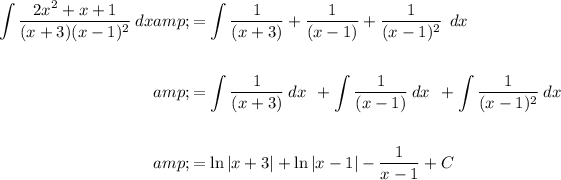Answer:
First, express the fraction in partial fractions
Write it out as an identity.
As the denominator has a repeated linear factor, the power of the repeated factor tells us the number of times the factor should appear in the partial fraction. A factor that is squared in the original denominator will appear in the denominator of two of the partial fractions - once squared and once just as it is:
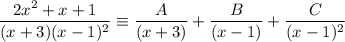
Add the partial fractions:
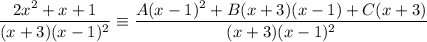
Cancel the denominators from both sides of the original identity, so the numerators are equal:
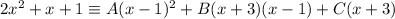
Now solve for A and C by substitution.
Substitute values of x which make one of the expressions equal zero (to eliminate all but one of A, B and C):
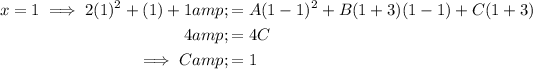
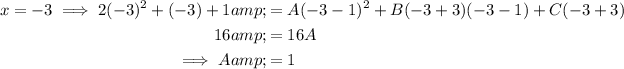
Find B by comparing coefficients:
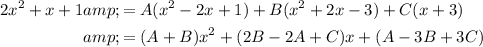
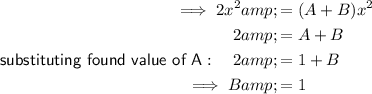
Replace the found values of A, B and C in the original identity:
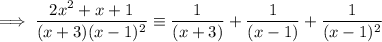
Now integrate: