Question

Gabriella invested $73,000 in an account paying an interest rate of 3%

compounded continuously. Mila invested $73,000 in an account paying an interest
rate of 3% compounded quarterly. After 5 years, how much more money would
Gabriella have in her account than Mila, to the nearest dollar?

Answer 1

Gabriella will make $61 more than Mila after 5 years

Explanation:

Gabriella Data

Principal Amount P= $73,000

Rate r = 3% or 0.03

Compounded continuously

Time t = 5 years

The formula used is:
`A=Pe^(rt)`

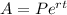
Putting values and finding A

`A=Pe^(rt)\\A=73000e^(0.03*5)\\A=73000e^(015)\\A=84813.899\\A\approx84814`

So, After 5 years Gabriella will have $84814

Mila Data:

Principal Amount P= $73,000

Rate r = 3% or 0.03

Compounded quarterly n = 4

Time t = 5 years

The formula used is:
`A=P(1+(r)/(n))^(nt)`

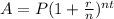
Putting values and finding A

`A=P(1+(r)/(n))^(nt)\\A=73000(1+(0.03)/(4))^(4*5)\\A= 73000(1+0.0075)^(20)\\A= 73000(1.0075)^(20)\\A=73000(1.161)\\A=84753`

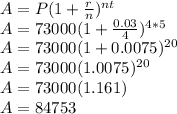
So, After 5 years Mila will have $84753

Now subtracting to find the difference 84814-84753 = 61

So, Gabriella will make $61 more than Mila after 5 years