Question

Why is the product of negative reciprocals always -1?

Answer 1

please check the explanation.

Explanation:

Let suppose we have a number = n

• n≠0

The negative reciprocal of 'n' = -1/n

Taking the product of 'n' and its negative reciprocal '-1/n':

`n\left(-(1)/(n)\right)`

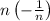
remove parentheses: (-a) = -a

`=-n(1)/(n)`

`\mathrm{Multiply\:fractions}:\quad \:a* (b)/(c)=(a\:* \:b)/(c)`

`=-(1* \:n)/(n)`

`\mathrm{Cancel\:the\:common\:factor:}\:n`

`=-1`

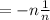
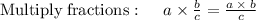
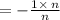
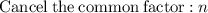
Canceling the common factor (the number itself) will bring -1.

It proves that the multiplication of any number and its negative reciprocal will always yield -1.