Question

Solve the system of equations by any method.



5x+9y =16
x+2y =4

Answer 1

The system of equations has one solution at (-4, 4).

Explanation:

We are given the system of equations:

`\displaystyle\left \{ {{5x+9y=16} \atop {x+2y=4}} \right.`

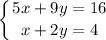
We can use elimination to solve this system. We need to multiply the second equation by -5 so we can cancel out our x-terms.

`-5*(x+2y=4) \rightarrow -5x - 10y = -20`

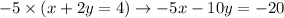
Therefore, our system now becomes:

`\displaystyle\left \{ {{5x+9y=16} \atop {-5x-10y=-20}} \right.`

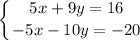
Now, we can add these two equations together and solve for y.

`\displaystyle(5x + 9y) + (-5x - 10y) = 0 - y\\\\16 + (-20) = -4\\\\-y = -4\\\\(-y)/(-1)=(-4)/(-1)\\\\y = 4`

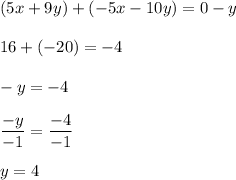
Now, we can substitute our value for y into one of the equations and solve for x.

`x+2(4)=4\\\\x + 8 = 4\\\\x = -4`

Therefore, our final solution is (-4, 4).