Answer:
22 units.
Explanation:
We want to find the perimeter of the polygon with vertices at: (-3, 1); (5, 1); (-3, 4); and (5, 4).
Let’s first plot the points and see what polygon we acquire. Please refer to the graph below.
As we can see, when plotting the points and connecting them, we get a rectangle.
So, we can use the perimeter formula for a rectangle, given by:
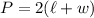
Where
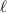Is the length and
is width.
Remember that the perimeter is simply the distance around the figure.
So, let’s find the length. We can do so by counting or by subtracting.
By counting, we can see that the length (longer side) is 8 units.
And by subtracting, we get the same length of |5-(-3)| or 8 units.
We use absolute value because distance is always positive.
Using the same process, we find the width to be 3 units.
Using subtract, we can see that this is indeed true as |1-4|=3.
So, we can now substitute the values into our formula:
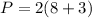
Evaluate:
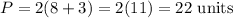
So, the perimeter of the polygon is 22 units.