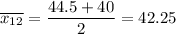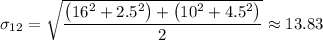Question

The weight of a suitcase checked onto a plane by a male, is a random variable with mean 42 pounds and standard deviation 16 pounds. The mean and standard deviation of the weight of a suitcase checked on to a plane by a female, is a random variable with mean 40 pounds and a standard deviation of 10 pounds. (For the purposes of this problem, a married couple consists of one male and one female. All suitcases are considered independent of each other even if from the same person.) What is the mean and standard deviation for the weight of the suitcases for a married couple, with one suitcase per person? What is the mean and standard deviation for the 6 suitcases checked onto the plan by 2 married couples, if each couple checked on 2 female suitcases and 1 male suitcase? In a cost cutting move the airlines is now charging $1.50 per pound for checked luggage. What is the mean and standard deviation for the cost of: A suitcase checked by a female 2 suitcases checked by a male. In an unexplained move, a worker at the airport adds a 5 pound graphing calculator to each male’s suitcase. What is the new mean and standard deviation for the weight of a male’s suitcase? What are the mean and standard deviation for the weight of the suitcases of a married couple, if the man’s suitcase is given the 5 pound calculator added to it?

Answer 1

1) The mean = 41

The standard deviation = 13.379

2) The mean = 40.67

The standard deviation = 12.365

3) The mean and standard deviation will remain the same

4) The new mean = 44.5

The new standard deviation = 13.58

5) The mean = 42.25

The standard deviation = 13.83

Explanation:

The combines mean is given by the formula;

`\overline {x_(12)} = (n_1 \bar x + n_2 \bar x)/(n_1 + n_2)`

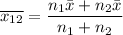
The combined standard deviation is given as follows;

`\sigma_(12) = \sqrt{(n_1 * \left (\sigma^2_(1) + d^2_1 \right) + n_2 * \left (\sigma^2_(2) + d^2_2 \right))/(n_1 + n_2) }`

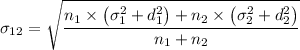
d₁ =
`\overline{x_(12)}` -
`\overline {x_1}`

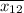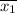
d₂ =
`\overline{x_(12)}` -
`\overline {x_2}`

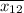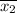
Substituting the known values, we have;

`\overline {x_(12)} = ( 42 + 40)/(2)=41`

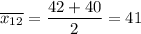
d₁ = 41 - 42 = -1

d₂ = 41 - 40 = 1

`\sigma_(12) = \sqrt{( \left (16^2 + 1 \right) + \left (10^2 +1 \right))/(2) } = 13.379`

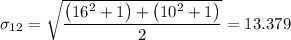
2) When n₁ = 1, n₂ = 2, we have;

`\overline {x_(12)} = ( 2 * 42 + 4 * 40)/(6) \approx 40.67`

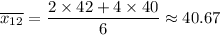
d₁ = 40.67 - 42 = -1.33

d₂ = 40.67 - 40 = 0.67

`\sigma_(12) = \sqrt{( 2 * \left (16^2 + 1.33^2 \right) + 4 * \left (10^2 +0.67^2 \right))/(6) } \approx 12.365`

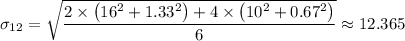
3) The mean and standard deviation will remain the same

4) The new mean = (42 + 47)/2 = 44.5

The new standard deviation
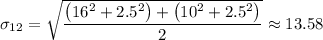
`\sigma_(12) = \sqrt{( \left (16^2 + 2.5^2\right) + \left (10^2 +2.5^2\right))/(2) } \approx 13.58`

5)
`\overline {x_(12)} = ( 44.5 + 40)/(2)=42.25`

`\sigma_(12) = \sqrt{( \left (16^2 + 2.5^2\right) + \left (10^2 +4.5^2\right))/(2) } \approx 13.83`